博文
清华笔记:计算共形几何讲义 (16)拓扑球面的调和映照
 精选
精选
|

【上课时间:每周二和周四上午9:50-11:20AM;地点:清华大学,近春园西楼三楼报告厅。欢迎任何有兴趣的朋友,前来旁听指导。】
上次课程,我们讲解了拓扑圆盘间的调和映照。这次,我们讨论拓扑球面间的调和映照。
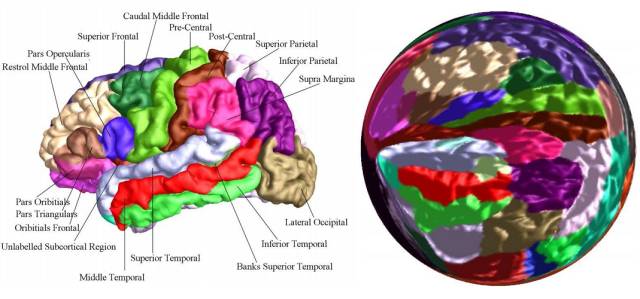
图1. 共形脑图。
拓扑球面间的调和映照在医学图像领域被频繁使用,特别是构造大脑皮层曲面到单位球面间的映射,我们称之为“共形脑图”,如图1所示。

图2. 拓扑球面间的调和映射。
非线性热流方法
图2显示了亏格为0的封闭曲面到单位球面间的调和映射。我们将源曲面想象成橡皮膜制成的曲面,目标曲面由表面抛光的大理石制成。我们将橡皮膜罩在大理石上,橡皮膜在抛光的大理石表面上自由无摩擦地滑动,当系统到达稳衡状态,橡皮膜的弹性形变势能达到最小,所得映射即为调和映射。这一物理图景启发我们设计拓扑球面调和映射的计算方法。
外蕴方法 我们将目标曲面单位球面嵌在三维欧式空间中,这样曲面间的映射可以被表示成从源曲面到三维欧式空间的映射,并且像集被限制在单位球面上,

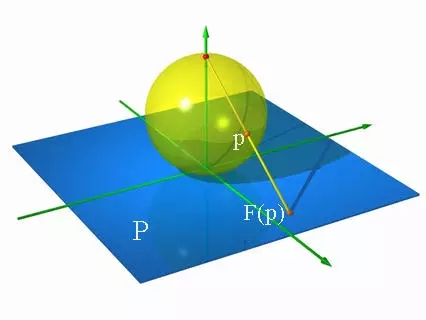
图3. 球极投影。
如图3所示,我们在单位球的北极放置一盏灯,从北极发射的光线将球面上所有点映到过南极的切平面上,同时将北极点映成无穷远点。直接计算表明,球极投影是共形映射。扩展复平面到自身的所有共形变换构成所谓的莫比乌斯变换群,每一个自映射都具有如下形式:


图4. 调和映射

图5. 共形映射
调和映照和共形映照的关系
图4和图5显示了从人脸曲面到单位圆盘的调和映射和共形映射。两个映射非常接近,但是如果我们仔细考察,我们发现在调和映射中,平面上的小圆被拉回到曲面上成为小椭圆(偏心率接近0);在共形映射中,平面上的小圆被拉回到曲面上成为小圆。
通常情况下,共形映射一定是调和的,调和映射不一定是共形的。在上图情形,当我们固定边界映射,优化调和能量,我们得到调和映射。如果,我们放开边界,令边界的像在单位圆上可以自由滑动,从而进一步减小调和能量,则我们得到共形映射。换言之,共形映射是所有调和映射中调和能量最小者。

黎曼映照的算法
利用拓扑球面间的调和映射,我们可以构造拓扑圆盘曲面间的共形映射,亦称是黎曼映射。假设源曲面是亏格为0的曲面,带有一条边界,边界足够光滑。我们取曲面的一个拷贝,将其定向取反,将两张曲面沿着边界上的对应点粘合,得到一张对称的拓扑球面。这一技术被称为是曲面的双重覆盖。我们用拓扑球面的调和映射将双重覆盖的曲面共形地映到单位球面上,然后复合一个莫比乌斯变换,使得原来曲面的边界被映成单位球面的赤道,再用球极投影将上半球面映成单位圆盘。由此,我们得到拓扑圆盘曲面的黎曼映射,如图4所示。
共形映射和调和能量
通过Hopf微分理论,我们知道保角映射一定是调和映射。更进一步,我们思考如下的问题:如果目标曲面上的曲率有正有负,那么同一同伦类中的调和映射有可能并不唯一,每一个调和映射都是调和能量的驻点,那么这些调和能量是否存在下界?假如存在共形映射,那么共形映射是否达到调和能量的下界?这两个问题的答案都是肯定的。


图6. Beltrami系数和伸缩商的几何意义。
我们考察从人脸曲面到平面单位圆盘的映射,如图6所示,映射将曲面上的无穷小椭圆映到平面的无穷小圆。无穷小椭圆的偏心率,就是伸缩商K,偏心率和椭圆长轴方向构成了Beltrami系数。从上面的推导我们可以看出,调和能量的下界等于目标曲面的面积;当所有的伸缩商K都是1时,调和能量的下界能够被达到,这时,映射为共形映射。
换言之,在所有可能的调和映射中,如果存在共形映射,则共形映射的调和能量达到全局最优。
调和映照唯一性

调和映照存在性

调和映照正则性

References
1. Xianfeng Gu, Yalin Wang, Tony F. Chan, Paul M. Thompson and Shing-Tung Yau. Genus Zero Surface Conformal Mapping and Its Application to Brain Surface Mapping. IEEE Transaction on Medical Imaging (TMI), 23(8):949-958, August 2004.
2. Craig Gotsman, Xianfeng Gu and Alla Sheffer. Fundamentals of Spherical Parameterization for 3D Meshes. ACM Transaction on Graphics (TOG), 22(3):358-363,2003.
https://blog.sciencenet.cn/blog-2472277-1197563.html
上一篇:清华笔记:计算共形几何讲义 (15)拓扑圆盘的调和映照
下一篇:清华笔记:计算共形几何讲义 (17)全纯二次微分(holomorphic quadratic differential)
全部作者的精选博文
- • 清华笔记:计算共形几何讲义 (23)离散曲面曲率流 (Discrete Surface Ricci Flow)V
- • 清华笔记:计算共形几何讲义 (22)离散曲面曲率流 (Discrete Surface Ricci Flow)IV
- • 清华笔记:计算共形几何讲义 (20)离散曲面曲率流 (Discrete Surface Ricci Flow)II
- • 清华笔记:计算共形几何讲义 (19)离散曲面曲率流 (Discrete Surface Ricci Flow ) I
- • 清华笔记:计算共形几何讲义 (18)拟共形映射(Quasi-Conformal Map)
- • 清华笔记:计算共形几何讲义 (17)全纯二次微分(holomorphic quadratic differential)
全部作者的其他最新博文
- • 清华笔记:计算共形几何讲义 (23)离散曲面曲率流 (Discrete Surface Ricci Flow)V
- • 清华笔记:计算共形几何讲义 (22)离散曲面曲率流 (Discrete Surface Ricci Flow)IV
- • 清华笔记:计算共形几何讲义 (21)离散曲面曲率流 (Discrete Surface Ricci Flow)III
- • 清华笔记:计算共形几何讲义 (20)离散曲面曲率流 (Discrete Surface Ricci Flow)II
- • 清华笔记:计算共形几何讲义 (19)离散曲面曲率流 (Discrete Surface Ricci Flow ) I
- • 清华笔记:计算共形几何讲义 (18)拟共形映射(Quasi-Conformal Map)