zhu2019-SIAM.Control.pdf  [作者：朱帅兵，周进，陈关荣，陆君安]

复杂网络的吸引域估计-中文介绍.pdf [注：本博文的PDF版本]

复杂网络的吸引域估计

[1] S. Zhu, J. Zhou, G. Chen, and J. Lu, “Estimating the region of attraction on a complex dynamical network,” SIAM J. Control Optim., vol. 57, no. 2, pp. 1189–1208, 2019.

Index Terms: Complex network, region of attraction (ROA), stability, synchronization, equilibrium point.

关键词：复杂网络，吸引域，稳定性，同步，平衡点.

一、引言

1.1 背景介绍. 同步是复杂动力网络中的一个基本问题，包括全局同步和局部同步。近十多年，人们更多地关注全局同步，而对局部同步的研究相对较少。值得注意的是，网络是否同步往往受初始条件的影响，例如对于如下含有2个节点的网络：

$$ \dot{x}_1 = f(x_1)+x_2-x_1, \hspace{3mm}   \dot{x}_2 = f(x_2)+x_1-x_2,  \hspace{2cm} (1)  $$

其中 f(x)=-x+x²。 若初值为 x₁(0)=2, x₂(0)=3, 网络（1）无法同步到 x₁=x₂=0, 尽管平衡点 x₁=x₂=0 是局部渐近稳定的；若 x₁(0)=0.2, x₂(0)=0.3, 网络（1）同步到 x₁=x₂=0。现有研究给出了局部同步的一些判据，但是没有给出初值的范围。因此，很有必要研究复杂网络的吸引域（ROA: region of attraction），即能够使得网络同步到某个给定平衡点的初始值的范围。通常，ROA的形状很不规则，只能找出它的尽可能大的子集。

1.2 研究动机. 现有文献中，ROA估计主要集中在两类系统：具有各种约束的线性系统和低维度的非线性系统。复杂网络通常具有高维度，而且节点动力学常常是非线性的，所以现有的一些方法无法直接应用到复杂网络的ROA估计。

1.3 主要贡献.（1）给出网络平衡点渐近稳定的一个充分条件和一个必要条件.（2）给出一般的ROA 估计方法，其中用到了方程解耦技巧以实现降维. 现有的解耦技巧需要假设耦合矩阵对称，我们首次把这一技巧推广到了非对称的耦合矩阵.（3）给出二阶的ROA估计方法。

二、准备工作

2.1 模型与分析. 考虑 N 个 n 维的节点构成的网络：

$$\dot{x}_i = f(x_i)+c\sum\limits_{j=1}^N a_{ij}h(x_j),\ 1\leq i\leq N \hspace{2cm}  (2)$$

其中，f, h 连续可微，c>0 为耦合强度，A=(a_ij)_N*N 为耦合矩阵。这里，A 只需满足行和为 0 的条件。令 s 为节点系统 x'=f(x) 的平衡点，则 S=[s^T, ..., s^T]^T∈R^nN 是网络(2)的平衡点。平衡点 S 的ROA定义为

$$ R_A = \left\{ X_0 \bigg| \lim_{t\to + \infty} X(t; X_0)=S \right\}, \hspace{2cm}  (3)$$

其中 X=[x₁^T, ... ,x_N^T]^T。我们的目标就是找到 R_A 的尽可能大的开子集。定义 e_i=x_i-s，则误差系统为

$$  \dot{e}_i =  f(x_i)-f(s)+c\sum\limits_{j=1}^N a_{ij}(h(x_j)-h(s))  =  F_1e_i+c\sum\limits_{j=1}^N a_{ij}F_2e_j+R_i^{(1)}+c\sum\limits_{j=1}^N a_{ij}R_j^{(2)},  \hspace{5mm}  (4)$$

其中，F₁=Df(s)，F₂=Dh(s)，R_i⁽¹⁾=f(x_i)-f(s)-F₁e_i，R_i⁽²⁾=h(x_i)-h(s)-F₂e_i。R_i^(k) 是泰勒展开的余项，也可以看作非线性部分。显然有 ||R_i^(k)||=o(||e_i||)。如果只研究平衡点的稳定性，可以忽略掉非线性部分R_i^(k)。但是，估计ROA需要用到非线性部分R_i^(k)。定义

$$\varphi_1(x)=\frac{\|f(s+x)-f(s)-F_1x\|}{\|x\|}, \hspace{3mm} \varphi_2(x)=\frac{\|h(s+x)-h(s)-F_2x\|}{\|x\|}, \hspace{2cm} (5)$$

则 ||φ_k(x)||=o(1)。(4)也可以写为

$$ \dot{e} = Ze+R^{(1)}+c(A\otimes I_n)R^{(2)}, \hspace{2cm}  (6)$$

其中，Z=I_N$\otimes$F₁+cA$\otimes$F₂，e=[e₁^T, ... ,e_N^T]^T，R^(k)=[R₁^(k)T, ... , R_N^(k)T]^T。记 A 的特征值为 λ₁, ... , λN，满足 |λ₁|≤ ... ≤|λ_N|。注意 A 不对称时 λi 可能为复数。

2.2 引理与假设. 

引理1. 可微函数 x, V 满足 a||x||²≤V(x)≤b||x||²，a,b>0. 对任意 δ∈(0, δ₀), 存在 β>0 满足

$$ \dot{V}(x(t)) \leq -\beta \|x(t)\|^2,\ \mathrm{if}\ \|x(t)\| \leq {\delta} $$

其中 δ₀>0。若 ||x(t₀)|| < r₀=$\sqrt{a/b}$δ₀，则 x(t) → 0.

引理2. 设 Ψ 的特征值为 ψ₁, ... , ψ_N。对任意 γ>0，存在矩阵 U∈ C^N*N 满足 Ψ=U^-1JU，其中

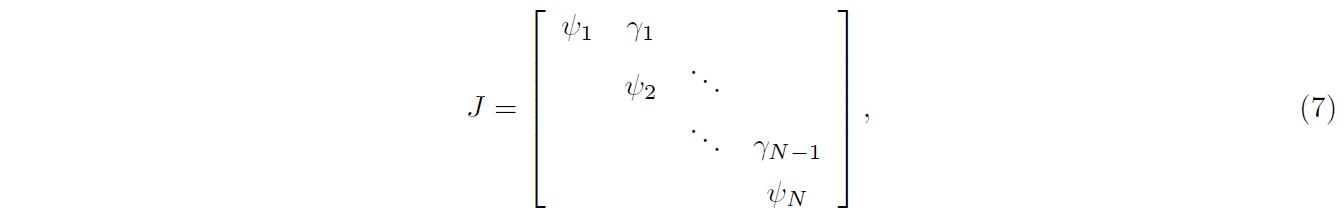
γ_i=0 或 γ。

    引理1可用于估计动力系统的吸引域。引理2可用于解耦高维的方程。当耦合矩阵 A 非对称时， A 可能无法对角化，但是一定可以化为若当型。若当型的次对角线元素为 0 或 1，不利于后续定理的证明。利用引理2，可以将 A 的次对角化为 0 或某指定的 γ。

假设1. (A1) 假设存在正定矩阵 P 和常数 ε>0 满足 PZ+Z^TP+εI_nN ≤ 0。

假设2. (A2) 假设存在正定矩阵 P=diag{P₁, ... ,P_N} 和常数 ε>0 满足

$$ P_i(F_1+c\lambda_i F_2)+(F_1+c\lambda_i F_2)^H P_i+\varepsilon I_{n} \leq 0. \hspace{2cm}  (8)$$

三、主要结果

3.1 稳定性分析.

定理1. 若(A1)成立，则网络(2)的平衡点 S 渐近稳定。

定理2. 若网络(2)的平衡点 S 渐近稳定，则节点系统 x'=f(x) 的平衡点 s 渐近稳定。

       定理1和定理2分别给出了网络(2)的平衡点 S 渐近稳定的一个充分条件和一个必要条件。现有文献中也有类似的充分条件，但是很少有文献给出必要条件。若节点系统的平衡点不渐近稳定，则由定理2立即得知网络系统的对应平衡点也不渐近稳定。

3.2 一般的ROA估计.

定理3. 考虑网络(2)。若(A1)成立，则

（a）对  ρ∈(0, 1), 存在正常数  δ₀=δ₀(ρ) 满足

$$ \varphi_k(x) < \nu_k, \ \forall x\in \mathrm{B}_{\delta_0}\backslash \{0\},\ k=1,2 $$

        $\nu_1=\frac{\varepsilon \rho }{2\|P\|}$，$\nu_2=\frac{\varepsilon (1-\rho)}{2c\|P\| \|A\|}$；

（b）$D=\left\{S+Y\left| \right.\|Y\| < r_0 \right\}$是 R_A 的子集，$r_0=\sqrt{ \lambda_{min}{(P)}/ \lambda_{max}{(P)} }\delta_0$。

    单个节点系统的维度通常比较小，所以一般来说找到定理3中的 δ₀ 比较容易。显然，δ₀ 的大小决定了所估计的ROA的大小。参数 ρ 取不同的值，可能得到不同的 δ₀。 寻找最优的 ρ 使得 δ₀ 最大的问题可以描述为

$$  \min   -\delta_0, \hspace{3mm}   \mathrm{s.t.}\ \varphi_1(x) < \nu_1, \hspace{1mm}  \varphi_2(x) < \nu_2, \hspace{3mm} \forall x \in \mathrm{B}_{\delta_0}\backslash \{0\},\   \rho \in (0,1). \hspace{2cm}  (9) $$

若 f, h 是线性的，则 φ₁=φ₂=0，此时 δ₀=+∞，D=R^nN，即平衡点 S 是全局渐近稳定的。

    定理3给出了一种估计网络(2)的ROA的简单方法。然而，当 N 很大时，不太容易找到(A1)中的 P, ε。因此，我们给出另一种估计方法，将(A1)的高维线性矩阵不等式（LMI）分解成了(A2)的 N 个低维的LMI。

定理4. 考虑网络(2)。若(A2)成立，则

（a）存在矩阵 U 满足 A=U^-1JU，其中 J 的形式如引理2所示，J_ii=λ_i，J_i,i+1=0 or $\frac{\varepsilon}{4c\|P\| \|F_2\|}$；

（b）对 ρ∈(0, 1)，存在正常数 δ₀=δ₀(ρ) 满足

$$\varphi_k(x) < \nu_k, \ \forall x\in \mathrm{B}_{\delta_0}\backslash \{0\}, $$

        $\nu_1=\frac{\varepsilon \rho }{4\|P\| \kappa_2(U)}$，$\nu_2=\frac{\varepsilon (1-\rho)}{4c\|P\| \|A\| \kappa_2(U)}$，$\kappa_2(U)$表示矩阵 U 的条件数；

（c）$D=\left\{S+Y\left| \right.\|Y\| < r_0 \right\}$是 R_A 的子集，$r_0=\sqrt{ \lambda_{min}{(P)}/ \lambda_{max}{(P)} } \frac{\delta_0}{\kappa_2(U)}$。

        定理4中计算 r₀ 的步骤如表1所示。定理4给出一种估计网络(2)的ROA的更加复杂但是也更加可行的方法。对于有向网络，耦合矩阵 A 不对称，所以 U 不是正交阵。定理4的估计一般情况下比定理3更保守，因为非正交的 U 使得$\kappa_2(U)$比较大。

推论1. 考虑网络(2)，假设其耦合矩阵 A 对称。若(A2)成立，则

（a）对 ρ∈(0, 1), 存在正常数 δ₀=δ₀(ρ) 满足

$$\varphi_k(x) < \nu_k, \ \forall x\in \mathrm{B}_{\delta_0}\backslash \{0\},$$

     $\nu_1=\frac{\varepsilon \rho }{2\|P\|}$，$\nu_2=\frac{\varepsilon (1-\rho)}{2c\|P\| \|A\|}$；

（b）$D=\left\{S+Y\left| \right.\|Y\| < r_0 \right\}$是 R_A 的子集，$r_0=\sqrt{ \lambda_{min}{(P)}/ \lambda_{max}{(P)} } \delta_0$。

        按照推论1计算 r₀ 的步骤与表1类似，除了不需要求解 U。推论1看起来和定理3几乎一样，但实际上是不同的。定理3中的 P, ε 通过解(A1)中不等式得到，而推论1则是通过解(A2)中不等式得到。

3.3 二阶ROA估计.

在表1中的步骤4，有时候不太容易确定最优的 ρ 。如果 f, h 二阶连续可微，则可以建立二阶的ROA估计方法，其不需要确定最优的 ρ 。接下来，假设 f, h 二阶连续可微。记

$$ f=[f_1,\cdots,f_n]^T,\ h=[h_1,\cdots,h_n]^T,\ R_i^{(k)}=[R_{i1}^{(k)},\cdots,R_{in}^{(k)}]^T. \hspace{2cm}  (10)$$

由于 f, h 二阶连续可微，有

$$ R_{ij}^{(k)}=\int_0^1 (1-\tau)e_i^T \Phi_j^{(k)}(s+\tau e_i)e_i\mathrm{d}\tau, \hspace{2cm}  (11)$$

其中$\Phi_j^{(1)},\Phi_j^{(2)}$ 分别是 f_j, h_j 的Hessian矩阵。假设

$$ \|\Phi_j^{(k)}(s+x)\| \leq \phi_{kj}(r),\ \forall x\in \overline{\mathrm{B}}_{r} $$

其中$\phi_{kj}$连续且非减。记$ \phi_k(r) = \sqrt{ \phi_{k1}^2(r)+ \phi_{k2}^2(r) + \cdots +  \phi_{kn}^2(r)}$。

定理5. 考虑网络(2)，假设(A1)成立。设 δ₀ 满足

$$\delta_0 \leq \sup \left\{\delta \in \mathbb{R} \left| \  \delta \|P\| \left(\phi_1(\delta)+c\|A\| \phi_2(\delta) \right) \right.\leq \varepsilon \right\},$$

则$D=\left\{S+Y\left| \right.\|Y\| < r_0 \right\}$是 R_A 的子集，$r_0=\sqrt{ \lambda_{min}{(P)}/ \lambda_{max}{(P)} } \delta_0$。

    对于ROA估计，很重要的一步是估计非线性部分 R^(k) 的上界。一般的ROA估计方法没有给出如何估计 R^(k)，而二阶的ROA估计方法提供了一种估计 R^(k) 的途径。

    仿照定理4和推论1，可以建立相应的二阶ROA估计方法。限于篇幅，这里不再一一列出。

四、数值仿真

考虑含有4个节点的有向网络，其中f(z)=(z₂, -r₁ sin z₁-b z₂)^T，h(z)=(z₁+r₂ sin z₂,z₂)^T，r₁ =1, b=2, r₂=0.1，c=0.25，

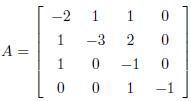
由于 A 非对称，利用定理4并按照表1的步骤估计平衡点 S=0 的ROA。

    限于篇幅，按照步骤1、2、3计算出的相关数据不再一一列出。步骤4中，φ_k估计如下：

$$ \|\varphi_k(z)\|= \frac{1}{\|z\|} {|r_k||z_{k}-\sin z_{k}|} = \frac{r_k}{\|z\|} (|z_{k}|-\sin|z_{k}|) \leq  r_k \left( 1-\frac{\sin\|z\|}{\|z\|} \right),\ k=1,2. $$

为了使 δ₀ 尽可能大，解如下的最优化问题：

$$  \min   -\delta_0, \hspace{3mm}   \mathrm{s.t.}\ r_1 \left( 1-\frac{\sin\|z\|}{\|z\|} \right) < 0.0570\rho, \hspace{1mm}  r_2 \left( 1-\frac{\sin\|z\|}{\|z\|} \right) < 0.0584(1-\rho), \hspace{3mm} \forall x \in \mathrm{B}_{\delta_0}\backslash \{0\},\   \rho \in (0,1). \hspace{2cm} $$

容易验证${0.0570\rho}/{r_1}={0.0584(1-\rho)}/{r_2}$时， δ₀ 达到最大。取 ρ=0.9112，得 δ₀=0.5625。因此，$D=\{X \left| \right.\|X\| < r_0=0.0906 \}$是 R_A 的一个子集。

        取初始值$x_i(0)=0.01[i-1,i+1]^T \in D$。 图1中左图显示网络的节点状态收敛到 S=0，与理论结果一致。取初始值$x_i(0)=3.14+0.5i+0.01[-1,1]^T \notin D$。 图1中右图显示网络的节点状态收敛到平衡点$(1,1,1,1)^T \otimes (2\pi,0)^T$而不是平衡点 S=0。这表明初始值不属于估计的吸引域 D 时，节点状态可能不收敛到给定的平衡点。

图1：网络的节点状态$x_{ij}\ (1\leq i\leq 4, 1\leq j\leq 2)$。左图中，初始值为$x_i(0)=0.01[i-1,i+1]^T \in D$；右图中，其中初始值为$x_i(0)=3.14+0.5i+0.01[-1,1]^T \notin D$。

五、结论

本文简要分析了复杂动力网络平衡点的渐近稳定性，并建立了一般的ROA估计方法和二阶ROA估计方法。尽管我们对ROA的估计可能还比较保守，但是我们的方法和结果迈出了研究复杂网络ROA估计的第一步。用其他形状（如椭球）估计ROA可能会得到更好的结果。将来的研究工作包括各种网络模型的ROA估计、对比估计的ROA与精确的ROA、估计不确定复杂网络的鲁棒ROA等。