Z(a)=Z(T)（$Z(a)\subseteq Z(T)$ is obvious, $Z(T)\subseteq Z(a)$:$\forall x\in Z(T),\forall g\in a,g=\sum g_{i}f_{i},g_{i}\in A,f_{i}\in T,$ we have $g(x)=0$ so $x\in Z(a)$）

A commutative ring R is called a Noetherian ring: if it satisfied one of the following conditions:

•  a ring in which every non-empty set of ideals has a maximal element. 
• a ring is Noetherian if it satisfies the ascending chain condition on ideals;
•  Every  ideal I in R is finitely generated, i.e. there exist elements a₁, ..., a_n in I such that I = Ra₁   + ... + Ra_n.
• Every non-empty set of ideals of R, partially ordered by inclusion, has a maximal element with respect to set inclusion.

Algebraic set: $Y=Z(T)$ for some T$\in$A

Proposition 1: $Z(T_{1})cup Z(T_{2})=Z(T_{1}cdot T_{2}))$ \ $cap_{alpha } Z(T_{alpha }) =Z(cup_{alpha }T_{alpha })\ emptyset=Z(1)\ A=Z(0)$

Zariski topology on Aⁿ :open sets is the complements of algebraic sets,by proposition 1 it is an topology. 

irreducible set: in a topology space a nonempty subset Y can not be the uion of two  proper subsets which are closed in Y 

Hausdorff space, separated space or T₂ space is a topological space in which distinct points have disjoint neighbourhoods

Examples: affine line A¹  with the Zariski topology :close set is the  set of zeros of a single polynomial .If the field k is algebraically closed ,the algebraic set must be the finite subsets.

$\bigstar$ A¹  is not Hausdorff.

$\bigstar$ A¹  is irreducible

Note: algebraically  closed field must be infinite.(if not ,0,1,$a_{1}\cdots a_{n}$be all the elements of $k$, $f(x)=x(x-1)(x-a_{1})\cdots (x-a_{n})-1)\in k[x]$,all the roots of $f(x)$ must in $k$,but 0,1,$a_{1}\cdots a_{n}$are all not the roots of $f$. Contradiction. )

$\bigstar$ $X$ is an irreducible topological space, $Y$ is an open subset in $X$  ,then $Y$ is also irreducible and $bar{Y}=X$ :

proof: we only need to show  the case $Y\neq X$. If $Y$ is not irreducible $Y=Y_{1}\cup Y_{2}$,we have $X=Z_{1}\cup Z_{2}$ where $Z_{i}=\bar{Y_{i}}\cup Y^{c}$,we claim that $Z_{i}$ are closed proper subsets of X.(it is easy to show the closeness, $Z_{i}\cap Y = Y_{i}$ are  proper subsets of Y ,hence they are proper subsets of $X.$)This is contradicted to $X$ is  irreducible.

If $\bar{Y}\neq X$,$X=\bar{Y}\cup Y^{c}$,then $X$ is not irreducible. Q.E.D

$\bigstar$ $Y$ is irreducible in $X$ ,then $bar{Y}$ is also irreducible in $X$.

(if not ,$\bar{Y}=Y_{1}\cup Y_{2}$, then $(Y_{1}\cap Y)\cup (Y_{2}\cap Y)=Y$,and $Y_{i}\cap Y$ are closed proper  subsets of Y(otherwise $Y\subset Y_{i}$ $\bar{Y_{i}}=\bar{Y}$ contradicte to $Y_{i}$ are proper subsets of $\bar{Y}$ ), Contradiction.)

Definition

$\bigstar$ Two important mappings $I$ $Z$ 

• $I$:$2^{A^{n}}\rightarrow 2^{A}$
• $Z$:$2^{A}\rightarrow 2^{A^{n}}$

Note :

1. $I$ maps any subset$Y$ of $A_{n}$ to an ideal of $A$ with the difinition$I(Y)=\{f\in A|f(P)=0 for all P\in Y \}$

Proposition1.2

(a).If $T_{1}\subset T_{2}$ ,then $Z(t_{2})\subset Z(T_{1})$

(b).If $Y_{1}\subset Y_{2}$ ,then $I(t_{2})\subset I(T_{1})$

(c).For any two subsets $Y_{1},Y_{2}$of $A^{n}$,$I(Y_{1}\cup Y_{2})=I(Y_{1})\cap I(Y_{2})$

(d).For any ideal 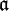$\subset A$,$I(Z(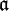))=\sqrt{a}$

(e).For any subset $Y\subset A^{n}$,$Z(I(Y))=\bar{Y}$

Proof:

转载本文请联系原作者获取授权，同时请注明本文来自孙旭明科学网博客。
链接地址：https://blog.sciencenet.cn/blog-636085-591560.html


下一篇：两个网站